The Tom Bearden
Website

 

TESLA'S SECRET AND THE SOVIET TESLA WEAPONS
  © T.E.  Bearden 1981
With Special Drawings by Hal Crawford


            Before the turn of the century, Nikola Tesla had discovered and was utilizing a new type of electric wave.  Tesla repeatedly stated his waves were non-Hertzian, and his wireless transmissions did not fall off as the square of the distance.  His discovery was apparently so fundamental (and his intent to provide free energy to all humankind was so clear) that it was responsible for the withdrawal of his financial backing, his deliberate isolation, and the gradual removal of his name from the history books. 
            By 1914 or so, Tesla had been successfully isolated and was already nearly a "nonperson."   Thereafter Tesla lived in nearly total seclusion, occasionally surfacing (at his annual birthday party for members of the press) to announce the discovery of an enormous new source of free energy, the perfection of wireless transmission of energy without losses, fireball weapons to destroy whole armies and thousands of airplanes at hundreds of miles distance, and a weapon (the "Tesla Shield," I've dubbed it ) that could provide an impenetrable defense and thus render war obsolete. 
               In my pursuit of Tesla's secret, it gradually became apparent to me that present orthodox electromagnetic theory is seriously flawed in some fundamental respects.  One of these is in the definition and use of φ, the scalar electrostatic potential.  It is this error which has hidden the long-sought unified field theory from the theorists. 
          In the theory of the scalar electrostatic potential (SEP), the idea is introduced of work accomplished on a charge brought in from a distance against the scalar field.  The SEP is not a vector field, but is a scalar field.  Indeed, scalar potential cannot of itself perform work on a charged mass; if it could do so, then tremendous force would exist on every mass due to the extremely high SEP of the vacuum itself.  Only a differential of SEP between two spatial points can produce force or accomplish work.  (Rigorously, a differential of scalar potential between two spatial points constitutes a vector.  Only a vector can produce force and do work.)
            Also, work can only be done on a mass.  Further, it takes time* to move an electron or other charged mass between two spatial points, and so the work performed by a spatial differential of the φ-field requires time.  Rigorously, the delta SEP is voltage, not SEP per se, and is directly related to E field.  The entire voltage concept depends on the work performed in moving a mass, after that mass has moved.  The idea of  "voltage" always implies the existence of a steady differential of φ between two spatial points for a finite length of time, and it also involves the assumption of a flow of actual mass having occurred.  SEP, on the one hand, is always a single-point function; on the other hand, difference in potential (i.e., V) is always a two point function, as is any vector. 
          Yet many graduate level physics and electromagnetics papers and texts erroneously confuse φ and V in the static case! Such an interpretation is of course quite incorrect. 

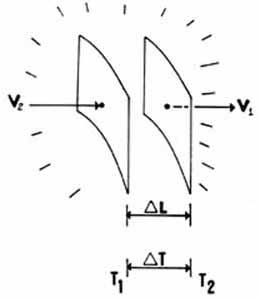
*  Two spatial points involve at least Δt = ΔL/c in time.  All vectors and gradients involve 2 separated spatial points, and thus present timelines in 4-space.  φ4 is a point, not a line, in 4-space.

          Another common assumption in present EM theory -- that the electrostatic potential (φ0) of the normal vacuum is zero -- has no legitimate basis.  In fact, we know φ0 is nonzero because the vacuum is filled with enormous amounts of fluctuating virtual state activity, including incredible charge fluctuations.  And by virtue of its point definition, φ0 must be the "instantaneous intensity" of these fluctuations -- but both in space and time.  The scalar electrostatic potential is therefore the "instantaneous stress" on spacetime itself, and a measure of the intensity of the virtual state flux through a 4-dimensional spacetime point. 
          Potential theory was largely developed in the 1800's, before the theory of relativity.  Time flowrate was then regarded as immutable.  Accordingly, electrostatic "intensity" was chosen as "spatial intensity," with the connotation of  "spatial flux density."  This assumes a constant, immutable rate of flow of time, which need not be true at all if we believe relativity.  Such a spatial "point" intensity is actually a "line" in 4-space, and not a 4-dimensional "point" at all.  Thus the spatial potential -- φ3 -- is a very special case of the real spacetime potential -- φ4, or charge and electromagnetic theory today is accordingly a special case of the real 4-space electromagnetism that actually exists!  Note also that charge is a 4-dimensional concept. 
          Now mass is a spatial, 3-dimensional concept.  Rigorously, mass does not exist in time -- masstime exists in time.  Mass and charge are thus of differing dimensionalities!
           Also, according to quantum mechanics, the charge of a particle -- e.g., of an electron -- is due to the continual flux of virtual particles given off and absorbed by the observable particle of mass.  Thus charge also is conceptually a measure of the virtual flux density, and directly related to φ.  Further, since the charge exists in time, it is the charge of a particle of spatial mass that gives it the property of masstime, or existing in time. 
           Here a great confusion and fundamental error has been thrown into the present EM theory by the equating of "charge" and "charged mass."  As we have seen, the two things are really very different indeed. 
          To speak of a spatial "amount" of charge erroneously limits the basic EM theory to a fixed time flowrate condition (which of course it was considered to be, prior to Einstein's development of relativity).  Thus when the limited present theory encounters a "relativistic" case (where the time flowrate changes), all sorts of extraordinary corrections must be introduced.  The real problem, of course, is with the fundamental definitions of electrostatic potential and charge.  The spatial "amount" of charge (i.e. the coulomb) as we presently erroneously use the term, is actually the spatial amount of observable "charged mass."  To correct the theory, one must introduce the true 4-space SEP and separate the definitions of charge and charged mass. 
          Only when a mass is moved does one have work --  and voltage or vector fields.  (The reason one has voltage and E field connected to a normal electrostatically charged object in the laboratory is because an excess of charged-particle masses are assembled on the object, and these masses are in violent motion!  A true static charge would have no E field at all. )

Table 1.  Some Present Theoretical Facts

  • Ø3-FIELD CONCEIVED BEFORE RELATIVITY

- POINT FUNCTION IN SPACE
- LINE FUNCTION IN SPACETIME
- TIME FLOWRATE CONSIDERED IMMUTABLE
- SPECIAL CASE OF Ø4, . . . . . .,ØN

  • GRADIENT BETWEEN TWO POINTS IN Ø3 FIELD

- PRODUCES VOLTAGE
- PRODUCES E FIELD
- MOVES ELECTRON
- IS AN AREA IN 4-SPACE

  • GRADIENT MAY BE BETWEEN SEPARATED POINTS IN TWO SUPERPOSED Ø-FIELDS

  • Ø-FIELD CAN "MOVE" AT INFINITE VELOCITY*

* JACKSON, CLASSICAL ELECTRODYNAMICS, 2ND EDITION, P. 223

 

Table 2.  Some Proposed Ø4 Characteristics

          φ-field need not involve observable mass accumulation, but only charge (virtual flowrate intensity) accumulation.  Accumulated masses are like so many gallons of water; accumulated charge is like so much pressure on both the water (space) and the time in which the water is existing. 
          Now, if one varies the SEP solely as a point function, one would have a purely scalar complex longitudinal wave, and not a vector wave at all.  This is the fundamentally new electrical wave that Tesla discovered in 1899. 
          Rigorously, all vector fields are two-point functions and thus decomposable into two scalar fields, as Whittaker showed in 1903.  It follows that any vector wave can be decomposed into two scalar waves.  By implication, therefore, a normal transverse EM vector wave, e.g., must simply be two coupled scalar (Tesla) waves -- and these scalars independently would be longitudinal if uncoupled.  An ordinary transverse EM vector wave is thus two pair-coupled Tesla scalar longitudinal waves, and only a single special case of the much more fundamental electromagnetics discovered by Nikola Tesla.
           A Tesla (scalar potential) wave -- i.e., a massless wave in pure φ0, the stress of the spacetime medium would have very strange characteristics indeed.  For one thing, since it moves in a complex 4-space, it has many more modes of movement than does a simple wave in 3-space.  And for another thing, it need not be bound at all by the speed of (vector) light.  In current theory, one φ3-field does not directly interact or couple with other existing φ3-fields except by simple superposition.  Therefore presently the φ-field is considered to have no drag limitation at all, hence infinite velocity.  (E.g., as stated in Jackson, Classical Electrodynamics, 2nd edition, page 223.)
          Actually, a φ4-wave can and will interact with some of the other existing φ4-waves in the medium transversed, and this interaction can involve pair-coupling into EM vector fields and waves, an interaction not presently in the electrodynamics theory.  The result of scalar pair-coupling creates a finite amount of vector "drag" on the φ4-wave, so it then has less than infinite velocity.  However, if this drag is small due to limited pair-coupling, the scalar wave's velocity through the slightly dragging medium still may be far greater than the speed of vector EM waves (light) in vacuum.  On the other hand, if the pair-coupling is made severe, the φ-wave may move at a speed considerably below the speed of vector light waves in vacuum.  The velocity of the φ4-wave is thus both variable and controllable or adjustable (e.g., simply by varying its initial amplitude, which through a given medium changes the percentage of pair-coupling and hence the degree of drag on the scalar wave).  The Tesla scalar wave thus can have either subluminal or superluminal velocity, in contradiction to present theory. 
          Note that the scalar wave also violates one of Einstein's fundamental postulates -- for the speed of our "new kind of light" wave is not limited to c, and need not be the same to every observer.  Thus Tesla scalar waves lead to a new "superrelativity" of which the present Einstein relativity is only a highly special case!

 

Table 3.  Tesla Waves Can:

  • ESTABLISH STANDING WAVES
          - in the earth
          - in the ionosphere

  • TAP ENERGY FROM THE EARTH'S CORE

  • TRAVEL FASTER OR SLOWER THAN LIGHT

  • CHANGE RATE OF TIME FLOW

  • AFFECT ALL FIELDS, INCLUDING GRAVITY

  • COMMUTE BETWEEN VIRTUAL AND OBSERVABLE

 

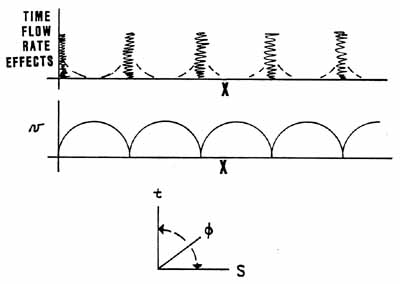
Figure 1.  Tesla's Standing Columnar Wave

          But let us now look for some subtle but real examples of scalar waves and scalar pair-coupling in nature.  As is well known, a tectonic fault zone can provide anomalous lights, sounds, etc. from stresses, piezoelectrical activity, and telluric currents in the earth and through the fault zone.  In examining the fault zone phenomena, I finally realized that a fault zone was literally a scalar interferometer i.e., if one can have scalar φ4-waves, they can interfere, either constructively or destructively.  Their interference, however, produces scalar pair-coupling into vector EM waves.  This coupling may be at a distance from the interferometer itself, and thus the interferometer can produce energy directly at a distance, without vector transmission through the intervening space.  Coupling of φ waves with the paired scalars comprising ordinary EM vector waves can also occur.  If this triplex coupling forms additional EM vector waves 180 degrees out of phase, the ordinary EM wave is diminished or extinguished.  If the scalar triplex coupling occurs so as to create vector EM waves in phase with the interacting vector EM wave, the amplitude of the ordinary vector wave is increased. 
          Scalar potential waves can thus augment or diminish, or create or destroy, ordinary EM waves at a distance by pair-coupling interference under appropriate conditions, and this is in consonance with the implications of Whittaker's fundamental 1903 work. 

 

ALL VECTORS AND
VECTOR FIELDS ARE CREATED
BY SCALAR INTERFEROMETRY
AND PAIR COUPLING

 

 

EM COUPLING CONDITION

        ΔL/c = ΔT

 

Figure 2.  Pair Coupling:  Producing EM at a Distance

 

 

EACH TINY STRESSED CRACK
ACTS AS A SCALAR INTERFEROMETER


LOCKED-IN STRESSED CRACKS

 

BECOMES A PRIGOGINE CRYSTAL

Figure 3.  Natural Scalar Interferometers

 

          An earthquake fault zone is such a scalar interferometer.  Stresses and charge pileups exist in the plates on each side adjacent to the fault, with stress relief existing in the middle in the fault fracture itself.  Since the rock is locally nonlinear, the mechanical stresses and electrical currents in it are also locally nonlinear.  This results in the generation of multiple frequencies of φ4-waves from each side of the fault interferometer, yielding two complex Fourier expansion patterns of scalar potential waves.  On occasion these two Fourier-transformed scalar wave patterns couple at a distance to produce stable ordinary electromagnetic field in a 3-dimensional spatial pattern -- e.g., a stress light such as the Vestigia light covered in Part I of The Excalibur Briefing.  Driven by the erratic two scalar Fourier expansion patterns of the scalar interferometer (whose input stresses normally slowly change), an erratic, darting, hovering "spooklight" of the variety studied by Vestigia is produced. 
          As the stresses change in each side of the interferometer, the distant scalar coupling zone is affected.  Thus the stresslight moves and its form changes, but it may be relatively stable in form for seconds or minutes.  Since the stresses in the rock may be intense, the stress light may involve an intense pair of φ-patterns coupling into the sphere or ball of vector EM energy.  The atoms and molecules of the air in the region of the coupled stresslight ball thus become highly excited, giving off radiant energy as the excited states decay. 
          Since much of the piezoelectric material in the stressed rocks is quartz grains, the features of quartz are of particular interest.  Each little quartz grain is itself highly stressed, and has stress cracks.  It is therefore a little scalar interferometer.  Further, quartz is transparent to infrared and ultraviolet; and the random orientation of all the quartz scalar interferometers may also form a Prigogine system far from thermodynamic equilibrium.  If so, this system can tap into highly energetic microscopic electromagnetic fluctuations to produce large-scale, ordered, relatively stable patterns of electromagnetic energy at a distance. 
          In short, all of this lends support to the formation of relatively stable but somewhat erratic patterns of electromagnetic energy at a distance from the fault itself.  In the atmosphere, such scalar interferometers could form in clouds or even in the air or between clouds and earth.  If so, such rare but occasional "weather" scalar interferometers could account for the rare phenomenon of ball lightning.  The intense energy of the ball of lightning, as compared to the lesser energy of an earthstress light, could well be due to the enormous electrical charges between clouds or between cloud and earth, available to fuel the scalar interferometer.  Very probably it is this phenomenon which gave Tesla the clue to scalar wave interferometry. 
          Thus such phenomena as earthstress lights, ball lightning, and the Tesla system of wireless transmission of energy at a distance with negligible losses and at speeds exceeding the speed of light may be explained.  They are complex, however, and involve fundamental changes to present electromagnetic theory.  These changes include utilizing 4-space scalar electrostatic potentials, scalar waves, pair coupling, ordinary 3-dimensional Fourier expansion, the Prigogine effect, and the properties of piezoelectric materials in rocks. 
          Since the scalar potential also stresses time, it can change the rate of flow of time itself.  Thus it affects anything which exists in time -- including the mind, both of the individual and at various levels of unconsciousness.  Therefore the same functions that result in earthstress lights also affect mind and thought, and are in turn affected by mind and thought.  This is the missing ingredient in Persinger's theory that UFO's are correlated with, and a result of, fault zones and earth stresses.  While Persinger seems to feel this is a "normal physics" explanation, it indeed involves a paranormal explanation. 
          The time-stressing ability of the true φ scalar wave also explains the interaction of such earthstress lights with humans and human intent, as noted by other researchers.  (E.g., the lights that repeatedly seemed to react to the observers, as detailed by Dr.  Harley Rutledge in his epoch-making Project Identification, Prentice-Hall, 1981.)
        These ideas in condensed form comprise the concepts required to violate the speed of light and produce an ordinary electromagnetic field at a distance, using scalar interferometry, without losses -- as Tesla had done in his wireless transmission system which he had tested prior to 1900 and had perfected by the 1930's.  Scalar interferometry can give stable regions of EM or "light energy" at a distance without losses, particularly as detailed in the beautiful Vestigia experiments, and it is within our grasp to utilize the new effects.  Indeed, any stress crack in a material can result in the scalar potential interferometer effect.  Exophoton and exoelectron emission -- poorly understood but already known in fatiguing of materials -- must be at least partly due to the scalar interferometer effect. 
          However, one additional caution should be advanced.  Normal movement of electrons allows so much "sideplay" movement of the electrons -- and there is so much such sideplay electron motion in the surrounding vicinity -- that pair coupling is almost instantaneous for small waves.  Thus orbital electrons in atoms seem to absorb and emit vector EM photons.  Actually they also emit some percentage of scalar waves as well.  Since a scalar wave is comprised exclusively of disturbance in the virtual state, it need not obey the conservation of energy law.  Further, a scalar wave of itself does not "push electrons" or other charges; hence it is nearly indetectable by present detectors.  Ionization detectors such as a Geiger counter tube, e.g., are exceptions if the scalar wave encountered is fairly strong.  In that case sufficient triplex coupling with the ionized gas occurs to produce additional ionization or charge, breaching the tube's cutoff threshold and producing a cascade discharge of electrons and voltage which is detected.  But weak scalar waves are presently indetectable by ordinary instruments.  However, these small scalar waves are detectable by sensitive interferometry techniques e.g., such as an electron interferometer.  Since the use of such instruments is quite rare, then indeed we have been living immersed in a sea of scalar waves without knowing it. 
          Finally, the percentage of scalar waves produced by changes in charged mass pileups can be increased by utilizing charged mass streaming.  Essentially the charged masses must be moved suddenly, as quickly as possible, at or near the complete breakdown of the medium.  For this reason, Tesla utilized sparkgaps in his early transmission systems, but also found that he could induce ionized media to "breakdown" in such fashion by a slow growth process.  One of his early patented atmospheric wireless transmission systems is based on this fact.  However, it was necessary to use a very high voltage, insuring extreme stress on the medium and hence some spillover stress onto time itself.  In other words, φ3 is always an approximation; at sufficiently high spatial stress, sufficient spillover φ4 exists to give Tesla scalar waves.  For this reason, Tesla used very high voltages and extremely sharp discharges to give "streaming" of the charged masses and thus high percentages of φ4 waves.  This suggests that the breakdown of dielectrics is a much richer phenomenon than is presently allowed for in the conventional theory. 
          To summarize, electrostatic potential -- φ-field is stress on the spacetime medium at a four-dimensional point.  I. e. , it is a sort of pressure on the medium, but pressure on all four dimensions, not just on the three spatial dimensions.  Thus in the new standard theory, φ4 may have complex values.  In addition, a φ-wave is to be interpreted as a scalar longitudinal wave in complex spacetime -- directly in φ0, the normal average 4-space stress itself.  And charge and charged mass must be recognized as two separate concepts.  This is the gist of what I finally recognized about Nikola Tesla's work and fundamental discovery. 
           This is exciting, for it means that Tesla stress waves can affect either space or time individually, or both space and time simultaneously, or even oscillate back and forth between primarily affecting time and primarily affecting space,  Tesla's waves were actually these φ-field scalar waves.  As such, they were fundamentally different from ordinary electromagnetic waves, and had entirely different characteristics, just as Tesla often stated.  E. g., a Tesla wave can either move spatially, with time flowing linearly; move temporally only (sitting at a point and waxing and waning in magnitude -- but changing the rate of flow of time itself in doing so, and affecting gravitational field, fundamental constants of nature, etc, ), or move in a combination of the two modes.  In the latter case, the Tesla wave moves in space with a very strange motion -- it oscillates between (1) spatially standing still and flexing time, and (2) moving smoothly in space while time flows smoothly and evenly.  I.e., It stands at one point (or at one columnar region), flexing for a moment; then slowly picks up spatial velocity until it is moving smoothly through space;  then slows down again to a "standing column," etc.  This is Tesla's fabulous "standing columnar wave."

Figure 4.  Exoelectric Emission

Figure 5.  The Tesla Effect


          Another wild characteristic of the Tesla wave is that it can affect the rate of flow of time itself; hence it can affect or change every other field including the gravitational field -- that exists in time flow.  It can also affect all universal constants, the mass of an object, the inertia of a body, and the mind and thoughts as well!  All of these exist in the flow of time, and they are affected if the time stream in which they exist is affected.  This was the awful secret that Tesla partially discovered by 1900, and which he came more and more to fully realize as he pursued its nature and its ramifications into the 1920's and 1930's. 
          Tesla also found he could set up standing φ-field waves through the earth.  He in fact intended to do so, for he had also discovered that all charges in the highly stressed earth regions in which such a standing wave existed produced φ-fields which would feed (kindle) energy into the standing φ-field wave by pair coupling.  I.e., normal vector field energy would "assemble" onto the scalar matrix wave by means of pair-coupling.  Thus by transmitting a scalar standing wave into the earth, he could easily tap the fiery scalar fields produced in the molten core of the planet itself, turning them into ordinary electromagnetic energy.  In such case, a single generator would enable anyone to put up a simple antenna and extract all the free energy desired. 
          When Tesla's alarmed financial backers discovered this was his real intent, they considered him a dangerous madman and found it necessary to ruthlessly stop him at all costs.  And so his financial support was withdrawn, he was harassed in his more subtle patent efforts (and the patents themselves were adulterated), and his name gradually was removed from all the electrical textbooks.  By 1914 Tesla, who had been the greatest inventor and scientist in the world, had become essentially a nonperson. 
          A few other persons in the early 1900's also were aware that potential and voltage are different.  And some of them even learned to utilize Tesla's φ-field, even though they only vaguely understood they were utilizing a fundamentally different kind of electromagnetic wave.  For example, James Harris Rogers patented an undersea and underground communications system which Tesla later confirmed utilized Tesla waves.  The U.S. secretly used the Rogers communications system in World War I to communicate with U.S. submarines underwater, and to communicate through the earth to the American Expeditionary Force Headquarters in Europe.  The Rogers system was declassified after the War and very shortly after that, it had mysteriously been scrubbed off the face of the earth.  Again, potential stress waves -- Tesla waves -- were eliminated and "buried."
         Probably the most brilliant inventor and researcher into Tesla's electromagnetics was T. Henry Moray of Salt Lake City, Utah.  Dr. Moray actually succeeded in tapping the limitless zero-point energy of vacuum (spacetime) itself.  By 1939, Dr. Moray's amplifier contained 29 stages and its output stage produced 50 kilowatts of power from vacuum.  Interestingly, another 50 kilowatts could be tapped off any other stage in the device -- which consequently could have produced almost 1.5 megawatts of electrical power!  Dr.  Moray's epoch-making work was suppressed also.  His device -- which represented over 20 years of heartbreaking accumulation of 29 working tubes from thousands made -- was destroyed by a Soviet agent in 1939, but not before the agent had obtained the drawings for building the tubes and the device itself.  Today the Moray amplifier is a standard component of many of the Soviet secret superweapons and Tesla weapons. 
           In the 20's and 30's, Tesla announced the final perfection of his wireless transmission of energy without losses even to interplanetary distances.  In several articles (e.g., H. Winfield Secor, "Tesla Maps Our Electrical Future, " Science and Invention, Vol. XVII, No.12, pp. 1077, 1124-1126), Tesla even revealed he used longitudinal stress waves in his wireless power transmission.  Quoting from the article, "Tesla upholds the startling theory formulated by him long ago, that the radio transmitters as now used, do not emit Hertz waves, as commonly believed, but waves of sound."  "He says that a Hertz wave would only be possible in a solid ether, but he has demonstrated already in 1897 that the ether is a gas, which can only transmit waves of sound; that is such as are propagated by alternate compressions and rarefactions of the medium in which transverse waves are absolutely impossible."  The wily Tesla did not reveal, of course, that such scalar waves nearly always immediately pair-coupled into vector waves when produced by normal means.  Tesla himself was working with longitudinal scalar waves. 

Table 4.  Rogers' Undersea and Underground Communication System

  • SECRETLY USED BY U.S. IN WWI

  • COMMUNICATED TO SUBS UNDERWATER
         - ANY DEPTH, UP TO 30 KHZ
         - REDUCED DEPTH, >30 KHZ

  • COMMUNICATED TO EXPEDITIONARY HQ OVERSEAS
         - 5,000 TIMES STRONGER THAN AERIAL
         - STATIC-FREE

  • DECLASSIFIED IN 1919
         - TO REVOLUTIONIZE COMMUNICATIONS
         - TO END ALL SURFACE ANTENNAS

  • MYSTERIOUSLY "LOST"

  • REDISCOVERED AND "LOST" THREE TIMES AFTER WWII

 

continued